Coin toss exercise

Advanced Statistical Inference

Simone Rossi

EURECOM

\[ \require{physics} \definecolor{input}{rgb}{0.42, 0.55, 0.74} \definecolor{params}{rgb}{0.51,0.70,0.40} \definecolor{output}{rgb}{0.843, 0.608, 0} \definecolor{vparams}{rgb}{0.58, 0, 0.83} \definecolor{noise}{rgb}{0.0, 0.48, 0.65} \definecolor{latent}{rgb}{0.8, 0.0, 0.8} \]

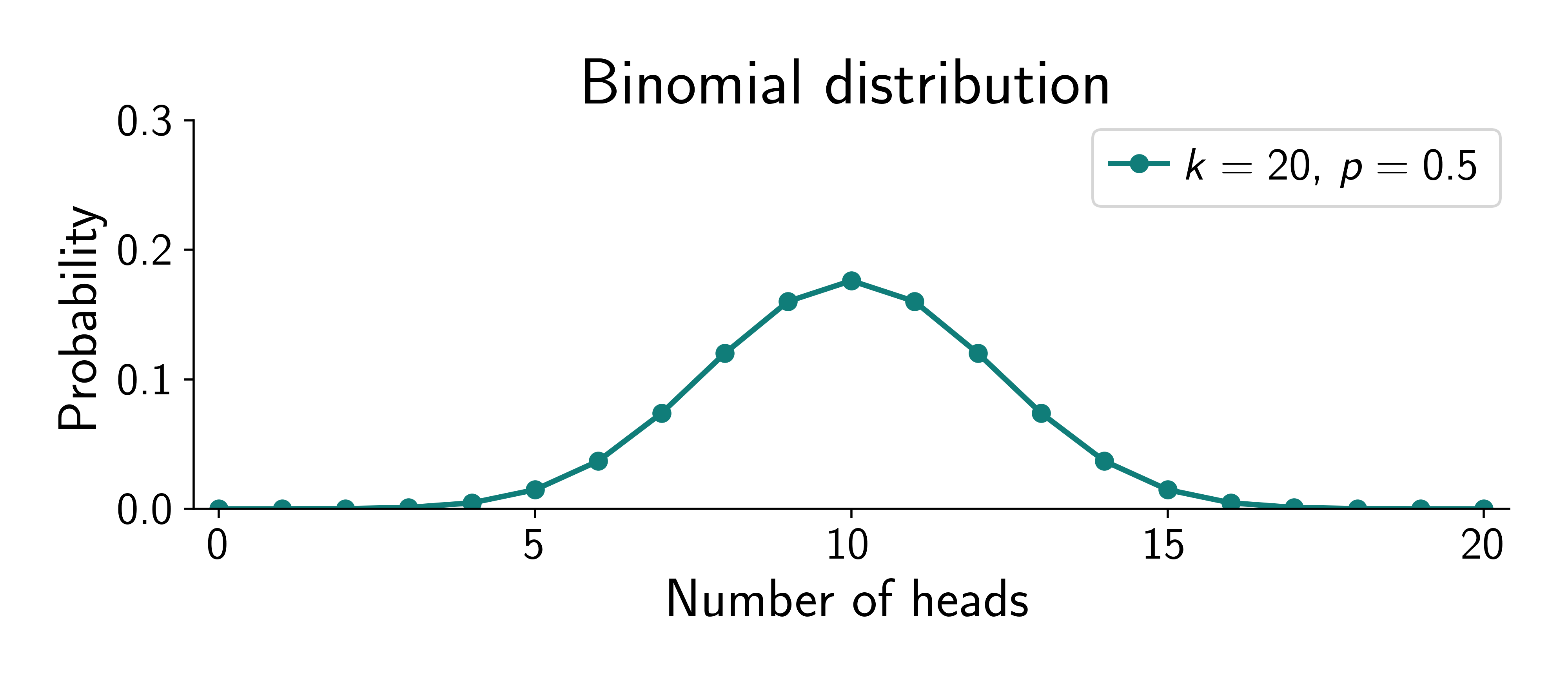
\[ \require{physics} \definecolor{input}{rgb}{0.42, 0.55, 0.74} \definecolor{params}{rgb}{0.51,0.70,0.40} \definecolor{output}{rgb}{0.843, 0.608, 0} \definecolor{vparams}{rgb}{0.58, 0, 0.83} \definecolor{noise}{rgb}{0.0, 0.48, 0.65} \definecolor{latent}{rgb}{0.8, 0.0, 0.8} \]

Coin toss: A class exercise

Problem statement

Setup: I toss the coin \(n\) times and observe \(\textcolor{output}{y}\) heads

Question: is the coin fair? What is the probability of heads?

Steps:

  1. Define a model for the number of heads
  2. Choose a prior distribution
  3. Compute the posterior distribution
  4. Make predictions

Model

Assumptions: (1) the probability of heads is the same for all tosses and (2) each coin toss is independent of the others.

We can model the number of heads \(\textcolor{output}{y}_n\) as a binomial distribution with probability \(\textcolor{params}{\theta}\):

\[ p(\textcolor{output}{y}\mid \textcolor{params}{\theta}) = \binom {n}{\textcolor{output}{y}} \textcolor{params}{\theta}^{\textcolor{output}{y}} (1-\textcolor{params}{\theta})^{n-\textcolor{output}{y}} \]

where \(\textcolor{params}{\theta}\) is the probability of heads, \(n\) is the number of tosses, \(\textcolor{output}{y}\) is the number of heads and \(\binom {n}{\textcolor{output}{y}}= \frac{n!}{\textcolor{output}{y}!(n-\textcolor{output}{y})!}\) is the binomial coefficient.

Prior

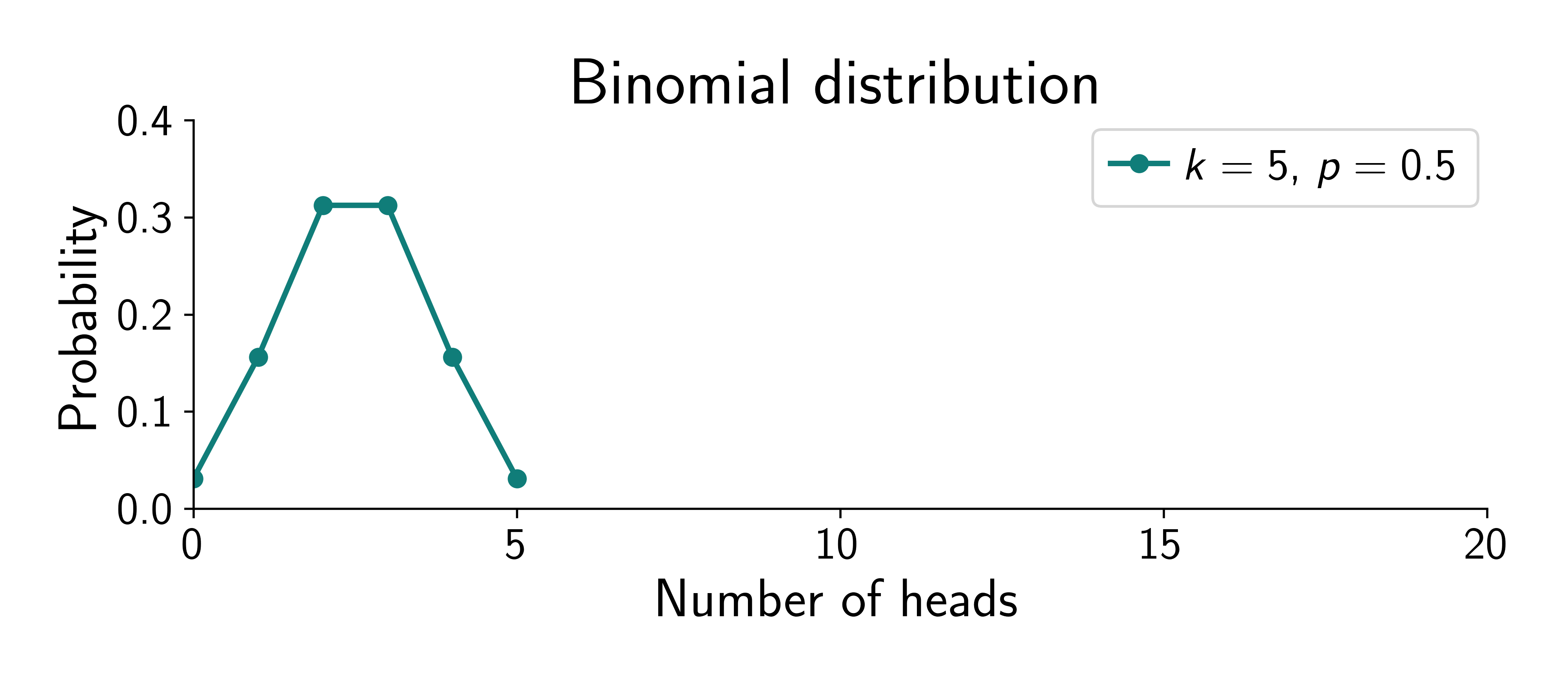
We need to specify a prior distribution for \(\textcolor{params}{\theta}\).

How to choose it? Remember what \(\textcolor{params}{\theta}\) represents: the probability of heads.

  1. It must be between 0 and 1.

  2. It must represent a continuous distribution.

  3. We want to be able to compute the posterior distribution (conjugate prior to the binomial distribution).

Beta distribution:

\[ p(\textcolor{params}{\theta}) = \frac{1}{B(\alpha, \beta)} \textcolor{params}{\theta}^{\alpha-1} (1-\textcolor{params}{\theta})^{\beta-1} \]

where \(B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\) is the beta function and \(\Gamma(\cdot)\) is the gamma function.

Two parameters: \(\alpha\) and \(\beta\). They represent our prior beliefs about the probability of heads.

  • If \(\alpha=\beta=1\), the beta distribution is uniform => we have no prior beliefs.
  • If \(\alpha=\beta>1\), we believe that heads and tails are equally likely, and the bigger the value, the more certain we are.
  • If \(\alpha > \beta\), we believe that heads are more likely.
  • If \(\alpha < \beta\), we believe that tails are more likely.

Posterior

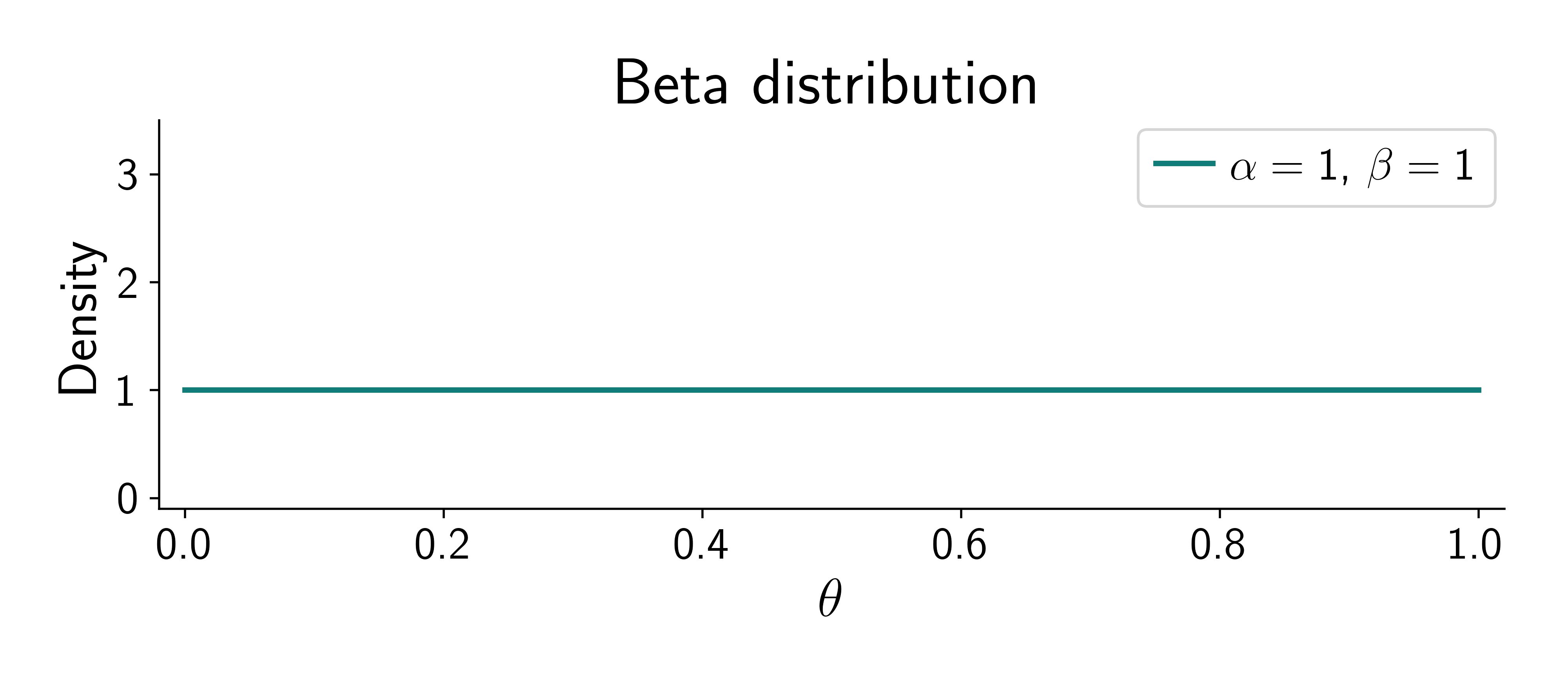
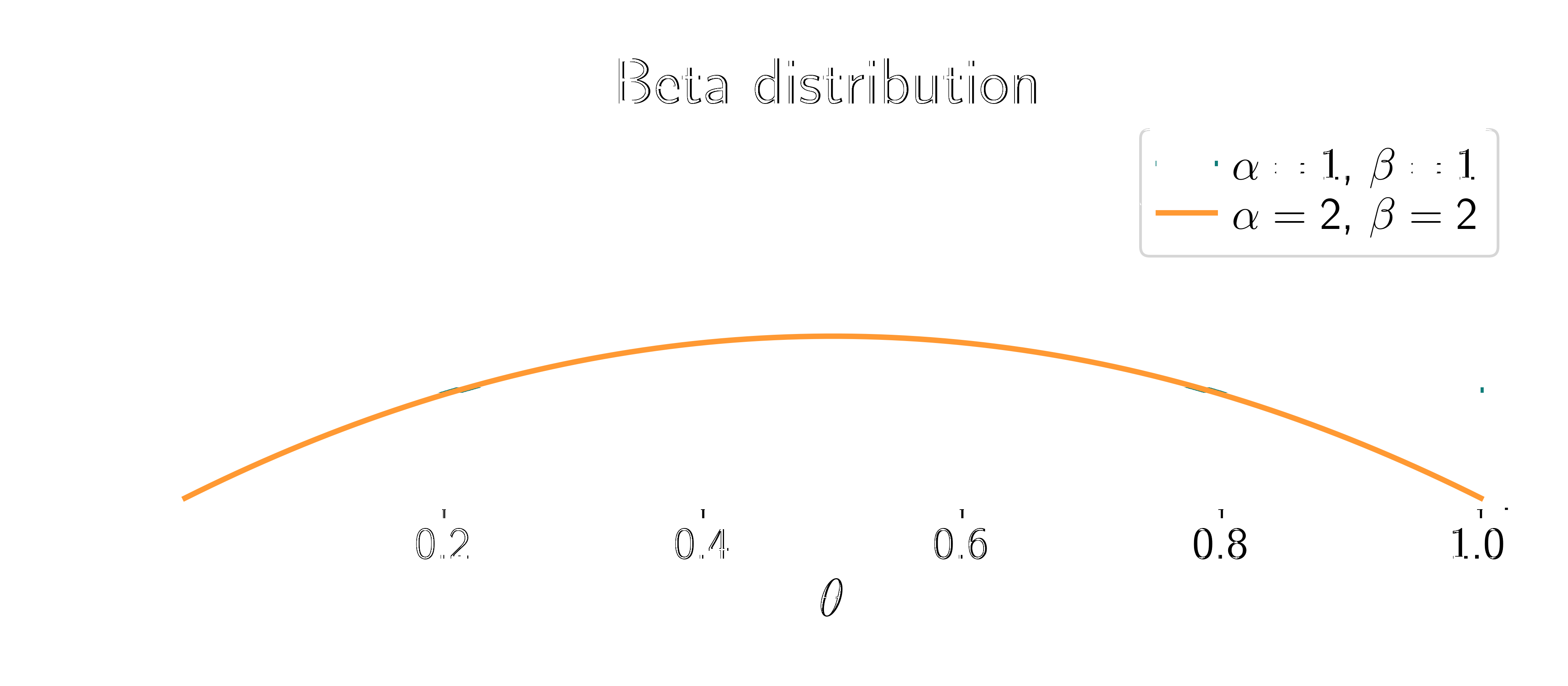
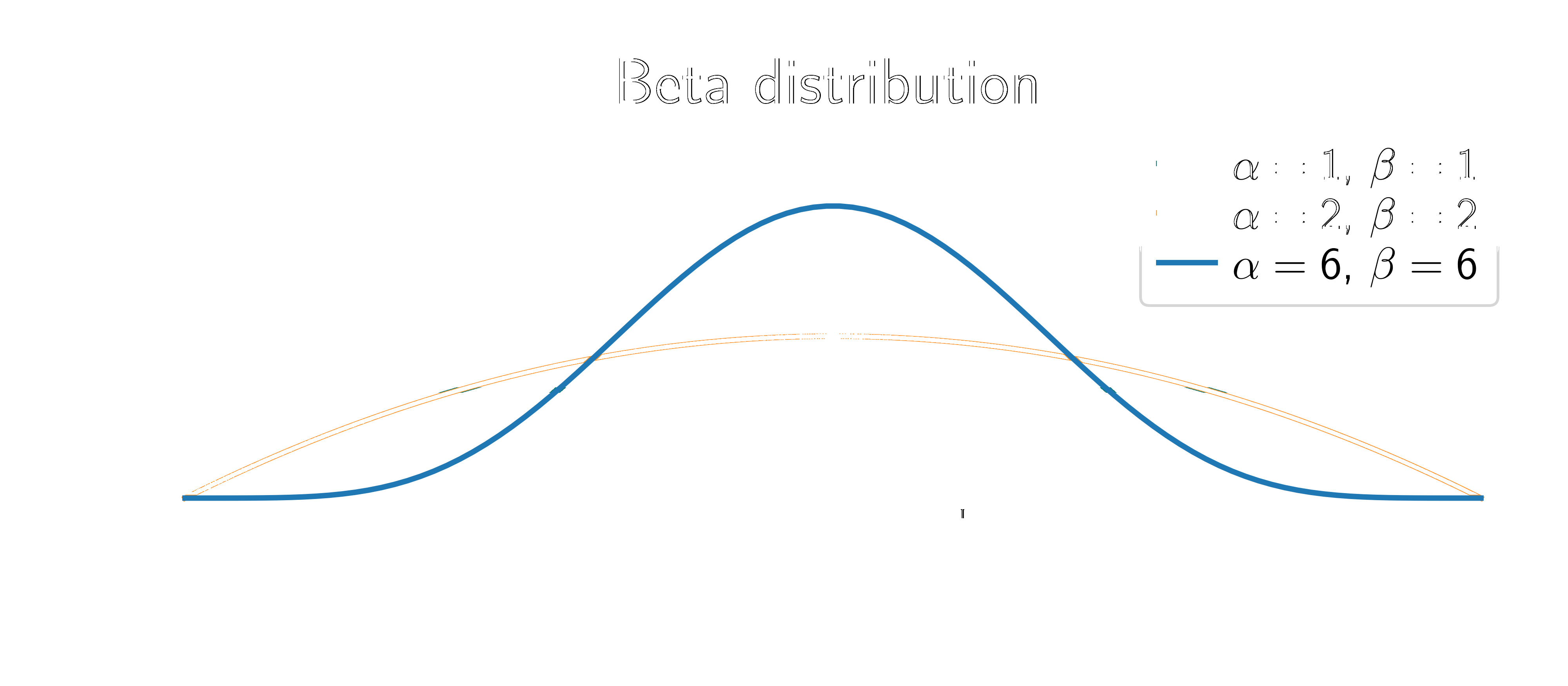
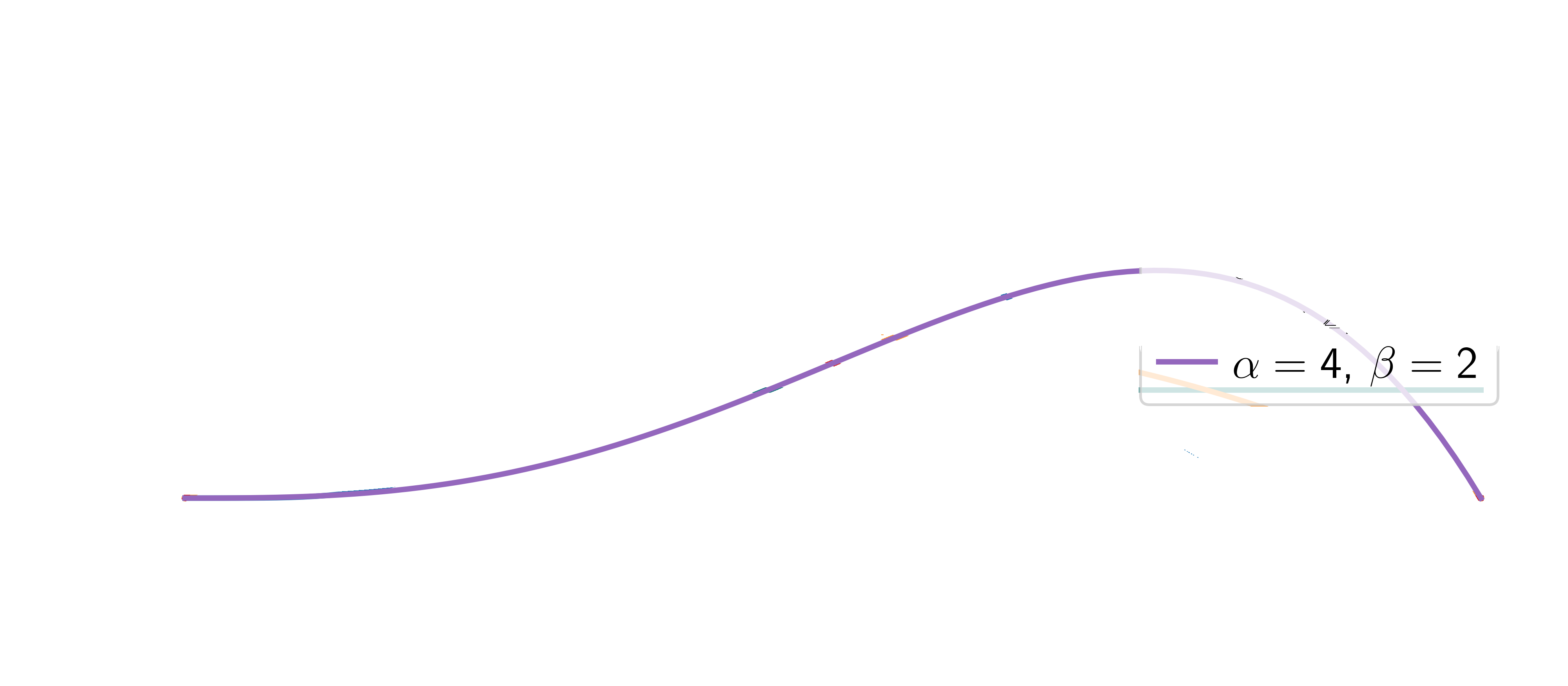
The posterior distribution is given by Bayes’ theorem:

\[ p(\textcolor{params}{\theta} \mid {\textcolor{output}{\boldsymbol{y}}}) = \frac{p({\textcolor{output}{\boldsymbol{y}}}\mid \textcolor{params}{\theta}) p(\textcolor{params}{\theta})}{p({\textcolor{output}{\boldsymbol{y}}})} \]

where \(p(\textcolor{output}{y})\) is the marginal likelihood (normalization constant).

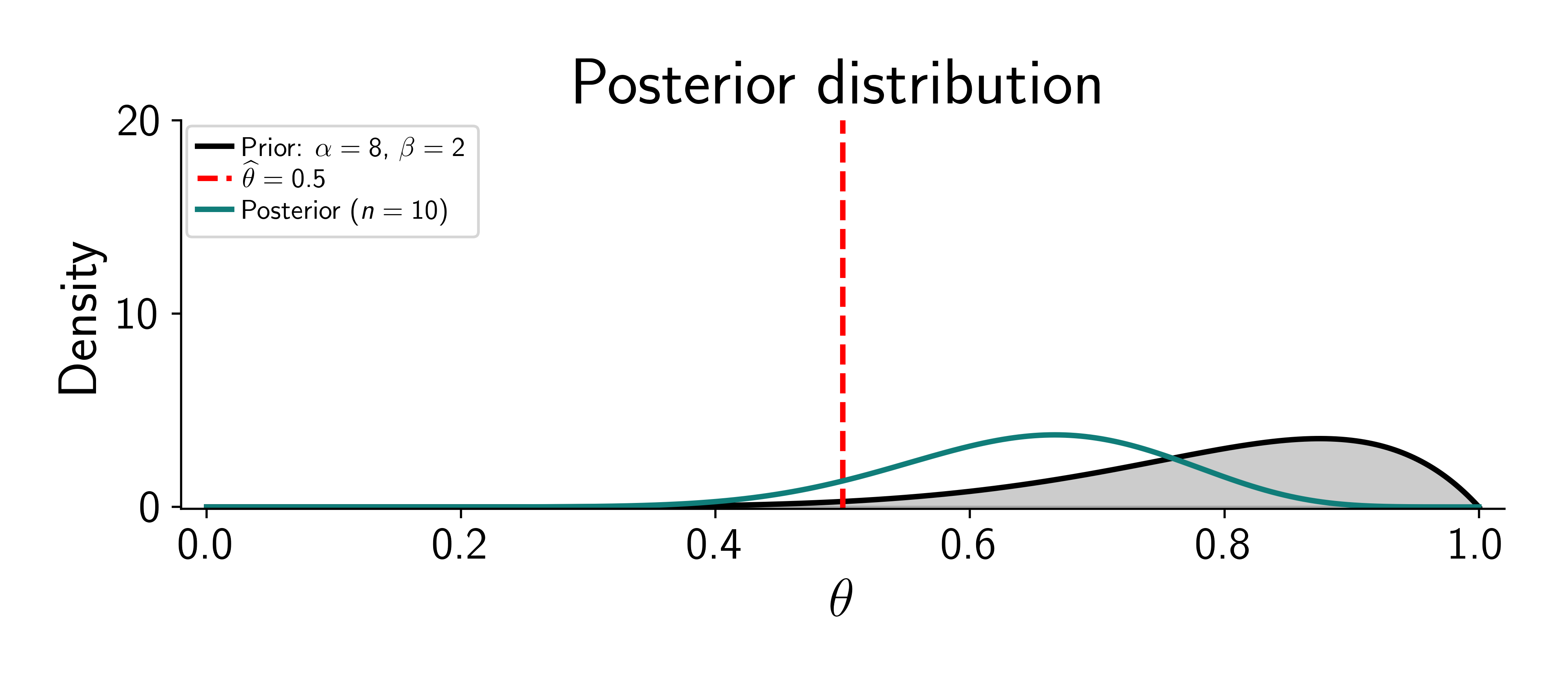
Because the beta distribution is the conjugate prior to the binomial distribution, the posterior is also a beta distribution:

\[ p(\textcolor{params}{\theta} \mid \textcolor{output}{y}) = \frac{1}{B(\alpha', \beta')} \textcolor{params}{\theta}^{\alpha'-1} (1-\textcolor{params}{\theta})^{\beta'-1} \]

We need to compute the new parameters \(\alpha'\) and \(\beta'\).

Posterior: computation of the parameters

From the conjugacy property, we have:

\[ p(\textcolor{params}{\theta} \mid \textcolor{output}{y}) = \frac{1}{B(\alpha', \beta')} \textcolor{params}{\theta}^{\alpha'-1} (1-\textcolor{params}{\theta})^{\beta'-1} \]

From Bayes’ theorem:

\[ p(\textcolor{params}{\theta} \mid \textcolor{output}{y}) \propto \textcolor{params}{\theta}^{\textcolor{output}{y}} (1-\textcolor{params}{\theta})^{n-\textcolor{output}{y}} \textcolor{params}{\theta}^{\alpha-1} (1-\textcolor{params}{\theta})^{\beta-1} \]

We can identify the parameters of the posterior distribution:

\[ \alpha' = \alpha + \textcolor{output}{y}, \quad \beta' = \beta + n - \textcolor{output}{y} \]

Concentrating the posterior

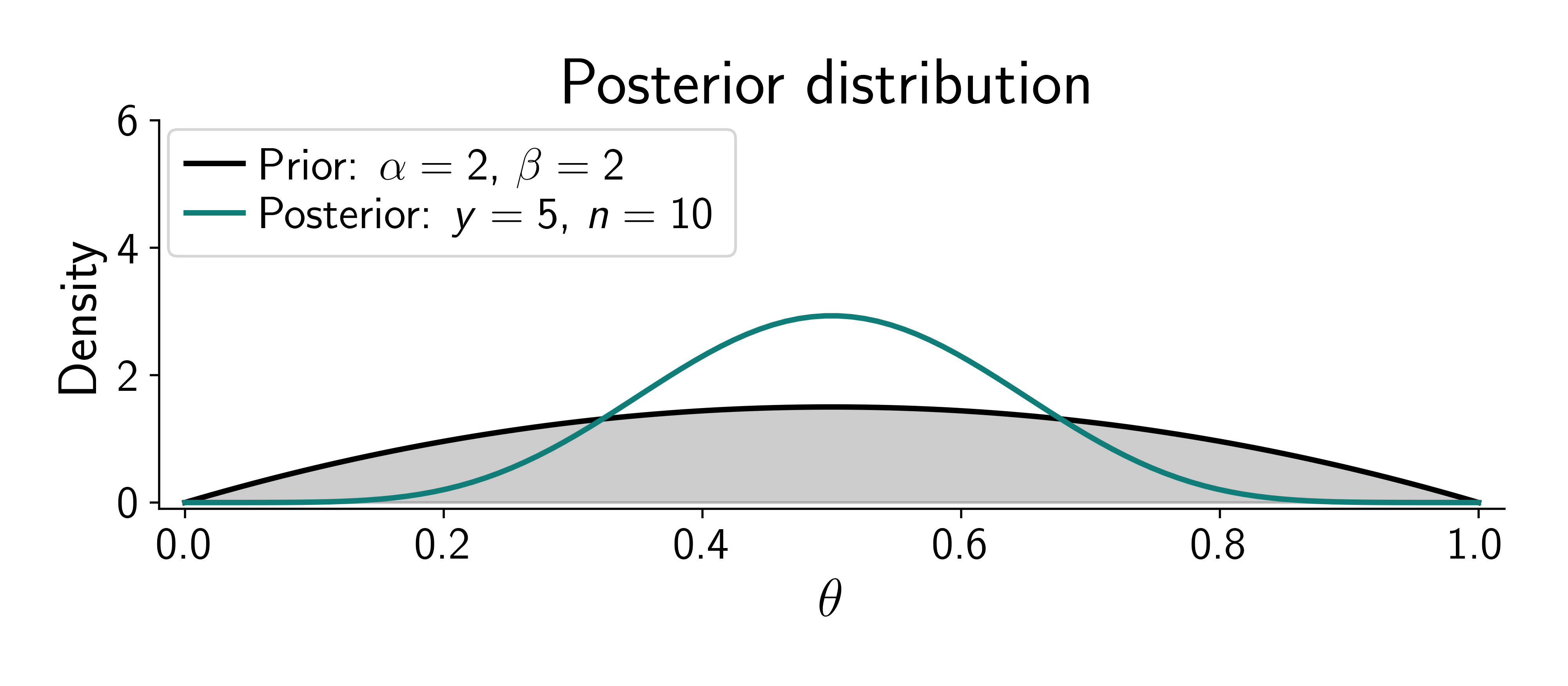
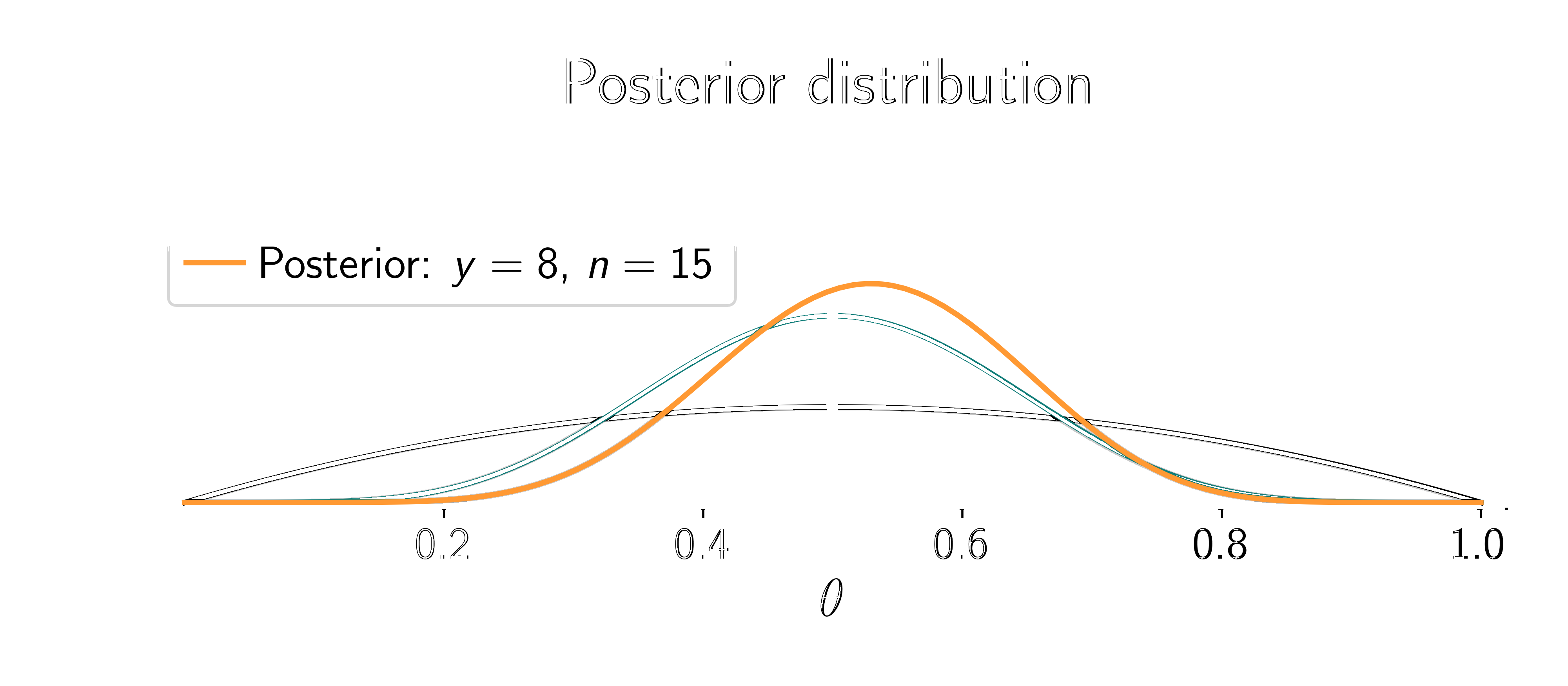
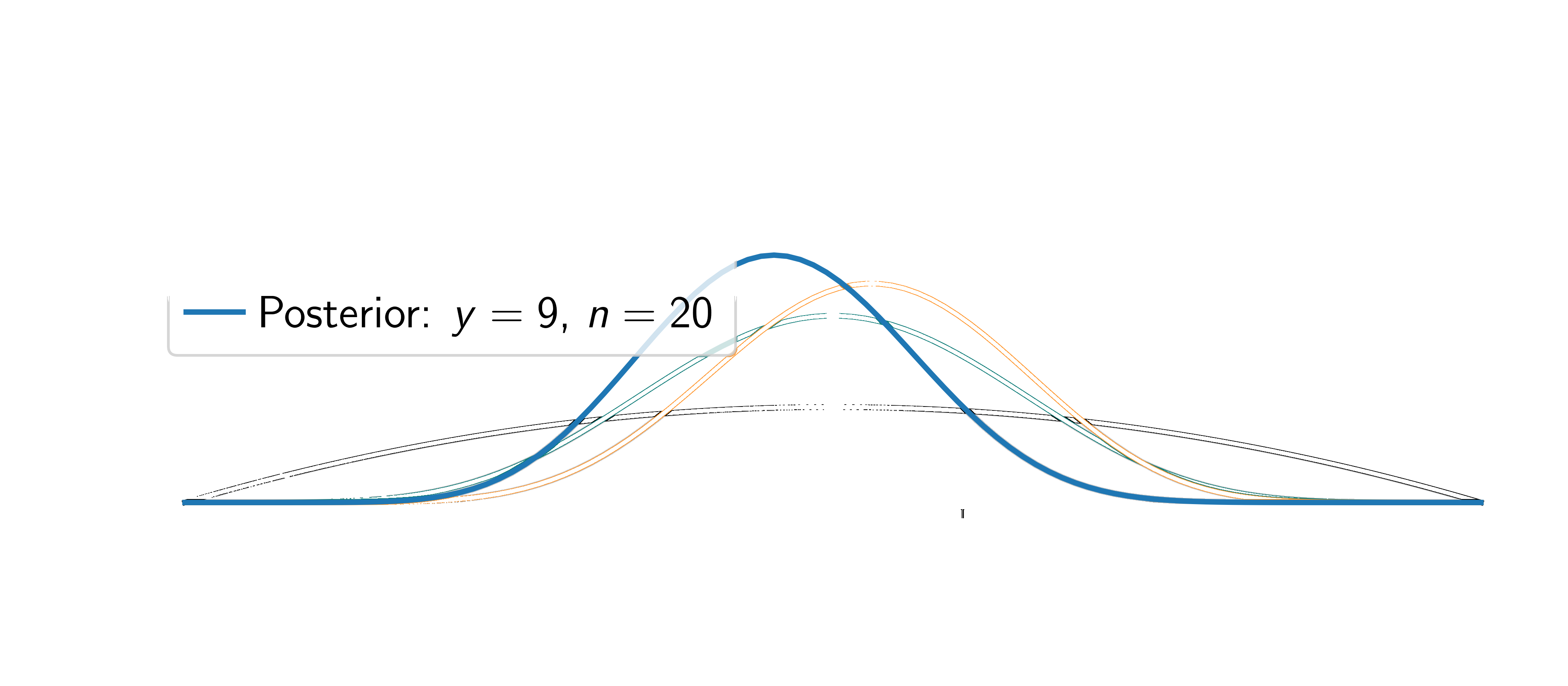
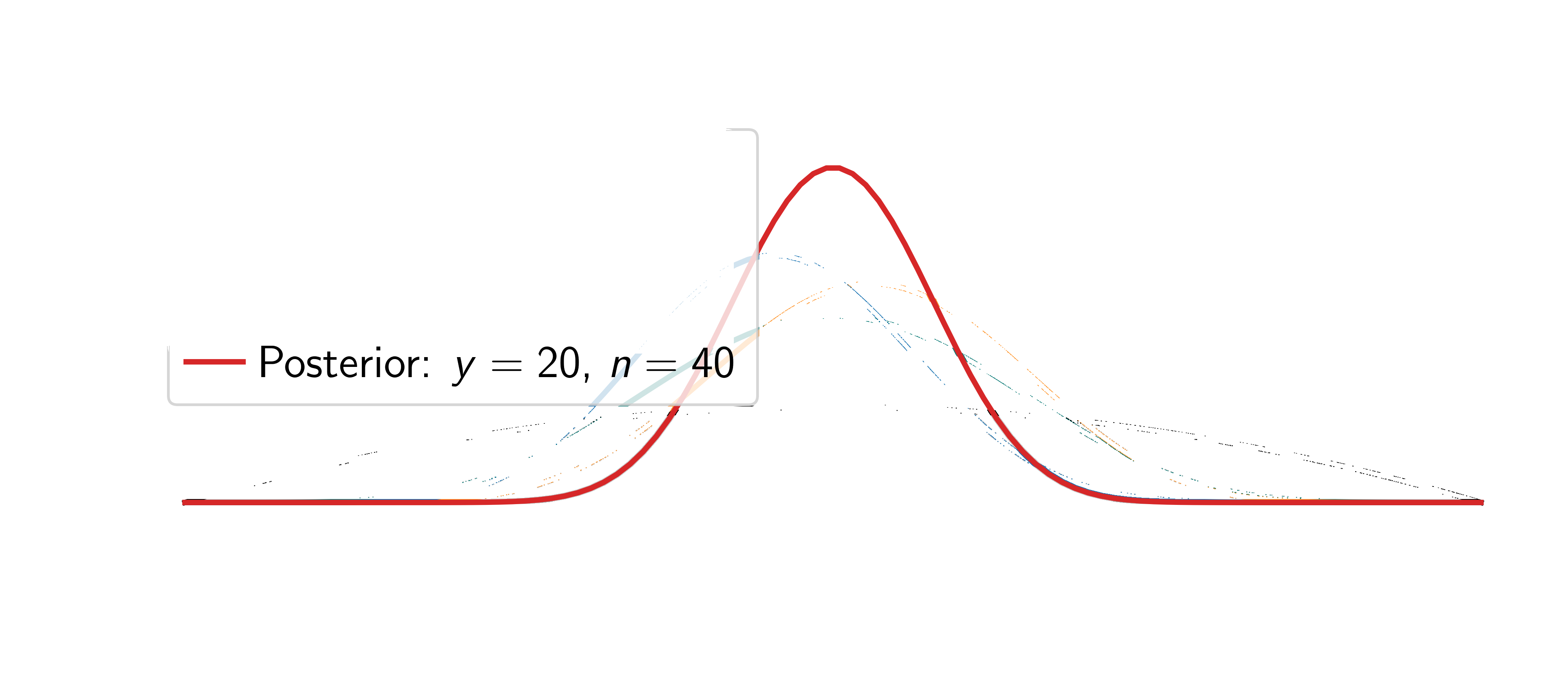
Assume the coin is fair (\(\textcolor{params}{\widehat\theta} = 0.5\)).

Two things happen:

  1. As we toss the coin more times, the posterior distribution becomes more concentrated around \(\textcolor{params}{\widehat\theta}\), regardless of the prior distribution.
  2. But the choice of the prior distribution tells us how fast this happens (how many data points we need).
  3. The posterior distribution looks more and more like a normal distribution.

Simone Rossi - Advanced Statistical Inference - EURECOM